Tiefe neuronale Netze können hochpräzise Vorhersagen liefern. Wenn sie aber Vorhersagen auf der Basis von Daten treffen sollen, die weit außerhalb der Verteilung der Trainingsdaten liegen, dann suggerieren viele Netzarchitekturen Vorhersagen mit übertrieben hoher Sicherheit. Für solche Daten sollte das Netz stattdessen schlicht ein „ich weiß es nicht“ als Antwort liefern.
Der Bayessche Ansatz greift diese Problematik auf. Benannt nach dem Mathematiker Thomas Bayes aus dem 18. Jahrhundert, bietet er einen grundlegenden Rahmen dafür, mit Unsicherheiten zu arbeiten. So ist es im Prinzip mathematisch möglich, eine A-posteriori-Unsicherheit zu den Gewichten der tiefen neuronalen Netze zu berechnen. In ihrer reinsten Form ist die Bayessche Inferenz aber leider oft unpraktikabel und nicht mit dem Computer ausrechenbar. Sogar Methoden, die die Rechenaufgabe nur annähern, sind für große Netze oft unzweckmäßig. Sie benötigen nicht nur viel Rechenkapazität, sondern sind auch schwierig zu programmieren.
Die Laplace-Approximation als anwenderfreundliche Möglichkeit der Unsicherheitsquantifizierung
Eine besonders einfache Form des Deep Learning mit näherungsweiser Bayesscher Berechnung erlangt gerade wieder Bekanntheit als schnelle, anwenderfreundliche Option zur Unsicherheitsquantifizierung. Denn sie funktioniert nicht nur in der Praxis gut, sondern bietet auch starke theoretische Garantien, wie wir in einer aktuellen Veröffentlichung zeigen.
Bei der sogeannten Laplace-Approximation handelt es sich um eine sehr alte und vergleichsweise einfache Idee. Deep-Learning-Algorithmen finden einen Gewichtungsvektor, der das Maximum einer Zielfunktion erreicht (blaue senkrechte Linie in Abb. 1). Die Laplace-Approximation identifiziert die Unsicherheit dieser Schätzung anhand der Krümmung der Zielfunktion um diesen Punkt herum: Eine schmale Spitze entspricht einer zuversichtlichen Schätzung der Gewichtung und eine breite Spitze einer wenig zuversichtlichen Schätzung. Diese Approximation ist natürlich nicht perfekt, da sie die tatsächliche Gewichtungsverteilung nur teilweise erfasst, so wie sich die grüne und die blaue Linie in Abb. 1 unterscheiden. In der Praxis reicht sie aber oft aus und liefert, obwohl sie so einfach ist, überraschend gute Ergebnisse. Verwendet man diese Approximation in Vorhersagen, wird aus dieser Unsicherheit für die Gewichte dann eine Unsicherheit für die Vorhersage (siehe Abb. 1).
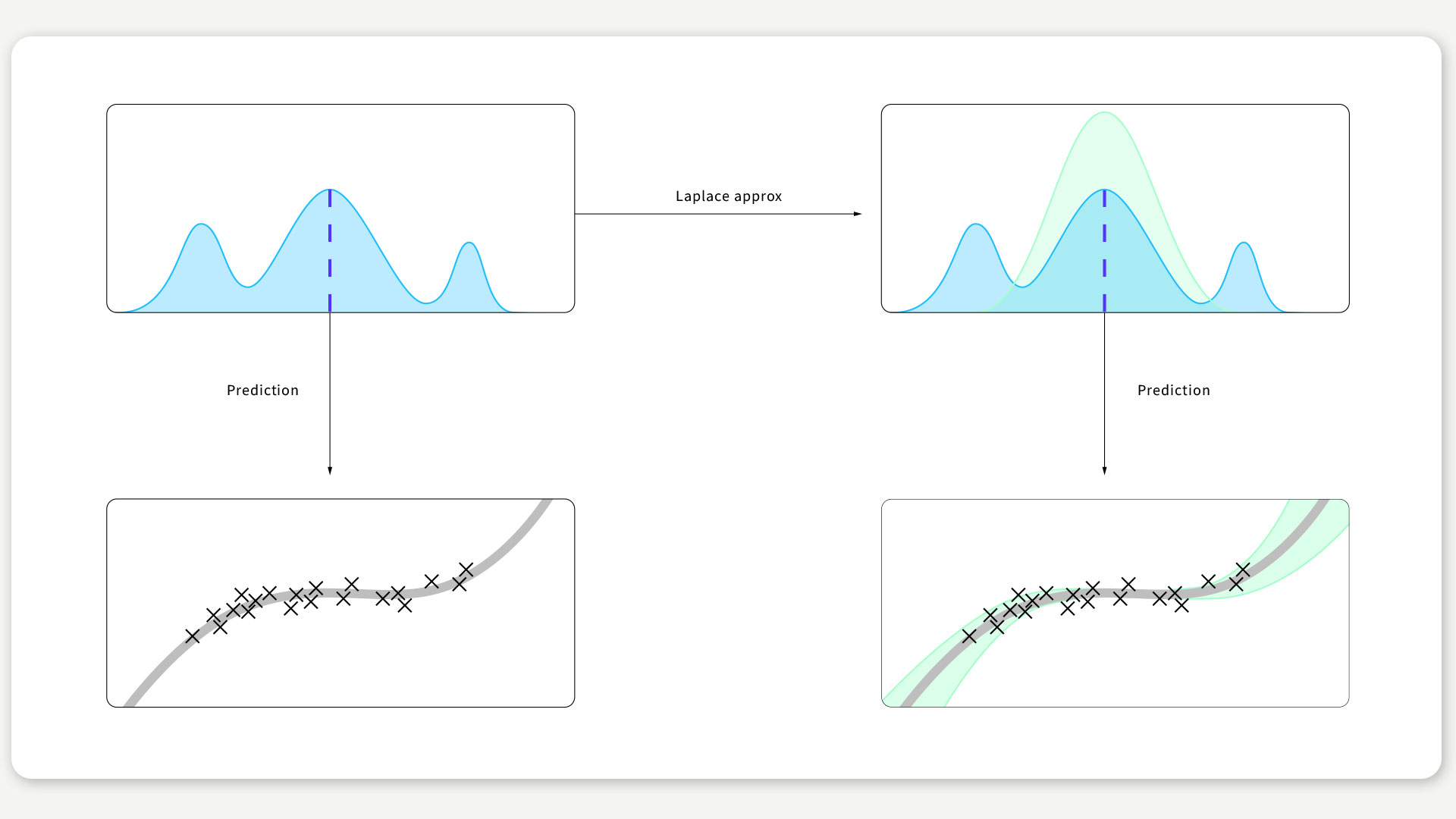
ABBILDUNG 1 / Oben: Die hellblaue Kurve ist die Zielfunktion. Die gestrichelte blaue Linie stellt eine durch Deep-Learning-Training erhaltene Schätzung dar. Bei der grünen Kurve handelt es sich um die Laplace-Approximation. Unten: Der grün schattierte Bereich stellt den Fehlerbalken der Vorhersage (graue Kurve) dar.
Die Genauigkeit der Netze wird nicht beeinträchtigt
In unserer kürzlich erschienen Arbeit zeigen wir, dass ein tiefes neuronales Netz auf extrem einfache Weise mit Unsicherheitsschätzungen ausgestattet werden kann. Das Netz wird wie üblich trainiert, anschließend wird lediglich die letzte Verarbeitungsschicht betrachtet und eine überschaubar kleine Matrix zweiter Ableitungen berechnet. Mit modernen Werkzeugen wie BackPACK, das in unserer Arbeitsgruppe entwickelt wurde, kann das mit nur wenigen zusätzlichen Zeilen Code erreicht werden (siehe Beispiel mit PyTorch unten). Das Ergebnis dieser Arbeit ist jetzt in einer Software-Bibliothek erhältlich, sodass Wissenschaftlerinnen und Anwender einen schnellen Einstieg in das Thema Unsicherheit in tiefen neuronalen Netzen bekommen.
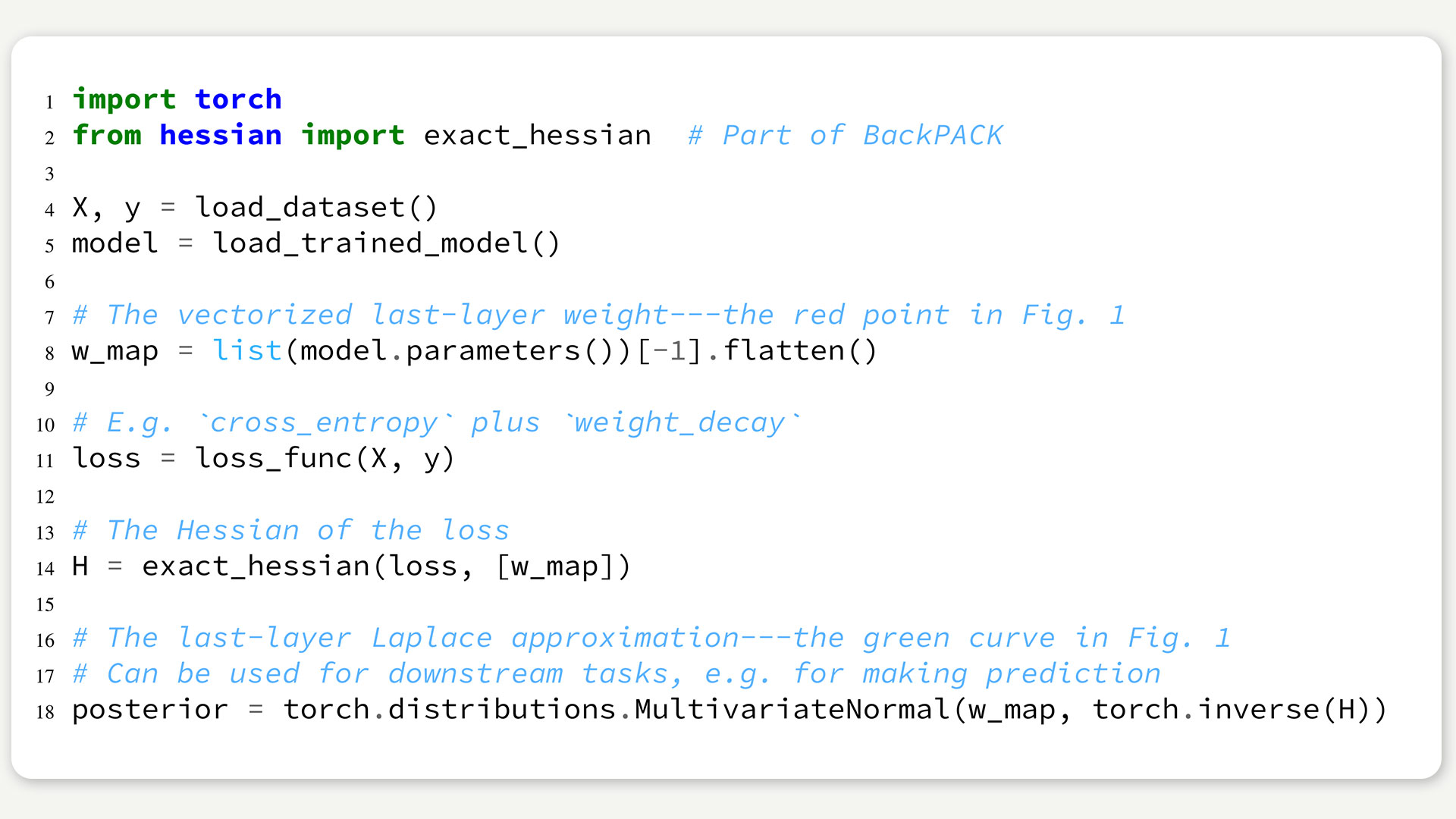
Das Besondere an diesem Verfahren: Im Gegensatz zu anderen Methoden kann es auf jedes vortrainierte tiefe neuronale Netz angewendet werden, ohne dessen Genauigkeit zu beeinträchtigen. Zudem können wir bei dem weit verbreiteten DNN-Modell mit ReLU-Aktivierungsfunktion zeigen, dass dieser Ansatz eine zu optimistische Einschätzung bei Daten, die weit außerhalb der Verteilung der Trainingsdaten liegen, verhindert (siehe Abbildung unten). Vollständige Code-Beispiele mit Schritt-für-Schritt-Erläuterungen sind hier und hier verfügbar.
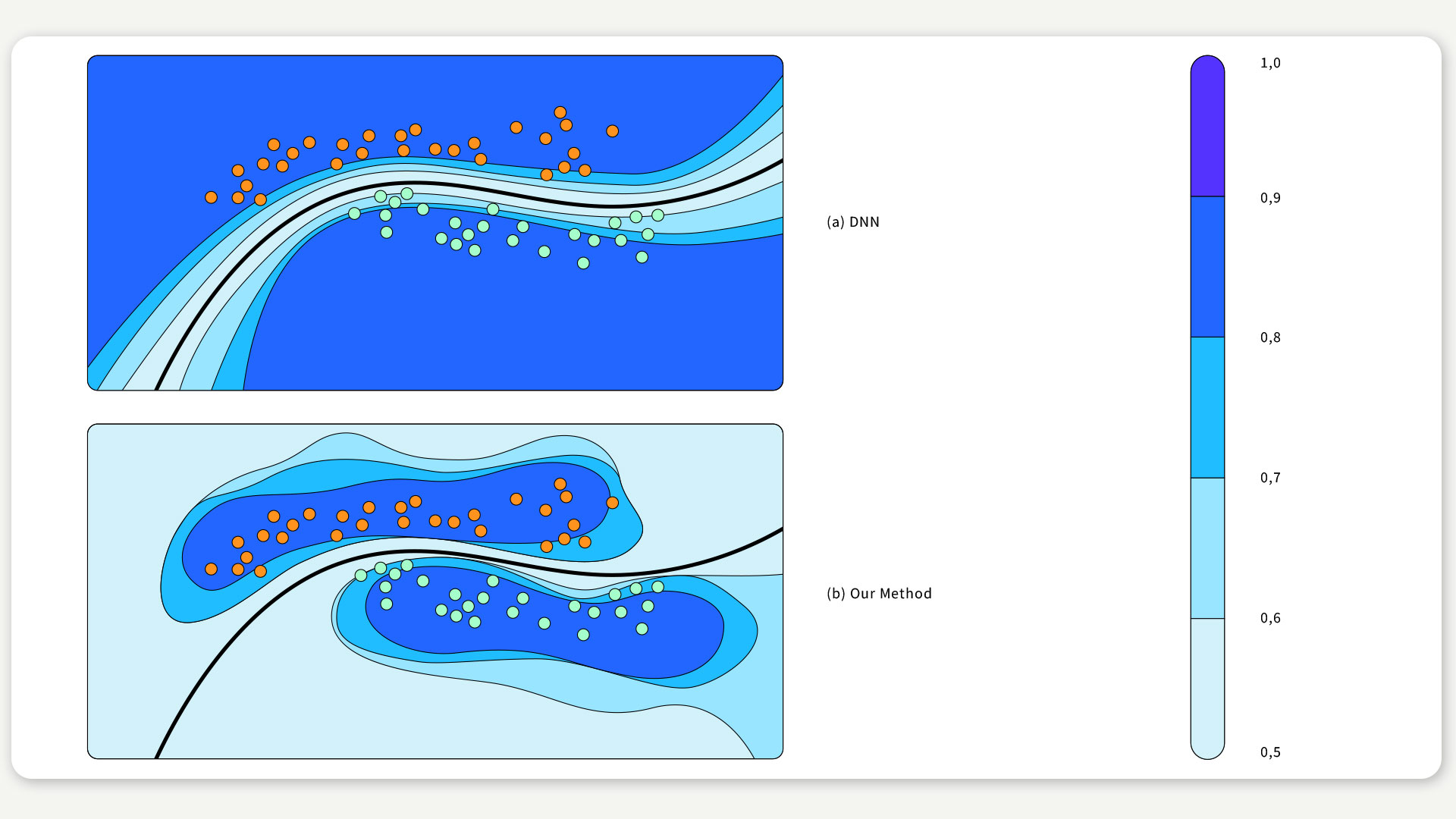
ABBILDUNG 2 / Anwendung unserer Methode bei einem Klassifizierungsproblem. Der schattierte Bereich zeigt die Schätzung des Konfidenzniveaus. Die schwarze Kurve ist die Entscheidungsgrenze.
Text: Agustinus Kristiadi, Philipp Hennig
Mitwirkung bei der Übersetzung ins Deutsche: Chris Richardson
Titelillustration: Franz Stämmele
Dieser Text bezieht sich auf folgende Arbeiten:
[1] Felix Dangel, Frederik Kunstner, and Philipp Hennig. BackPACK: Packing more into Backprop. In ICLR, 2020.
[2] Matthias Hein, Maksym Andriushchenko, and Julian Bitterwolf. Why ReLU Networks Yield High-confidence Predictions Far Away from the Training Data and How to Mitigate the Problem. In CVPR, 2019.
[3] Geoffrey E Hinton and Drew Van Camp. Keeping the neural networks simple by minimizing the description length of the weights. In Proceedings of the sixth annual conference on Computational learning theory, pages 5–13. ACM, 1993.
[4] David JC MacKay. A practical bayesian framework for backpropagation networks. Neural computation, 4(3):448–472, 1992.
[5] Radford M Neal. Bayesian learning via stochastic dynamics. In Advances in neural information processing systems, pages 475–482, 1993.
[6] Anh Nguyen, Jason Yosinski, and Jeff Clune. Deep neural networks are easily fooled: High confidence predictions for unrecognizable images. In CVPR, 20157

Mit maschinellem Lernen Modelle in der Neurowissenschaft identifizieren


Kommentare