Diffusion ist in unserem Alltag ein allgegenwärtiger Prozess. Wenn wir unsere Pflanzen gießen, diffundiert Wasser durch den Boden. Wenn wir ein Steak braten, lassen wir Hitze hindurchdiffundieren. Und wenn wir uns auf Corona testen, diffundieren chemische Reagenzien durch den Teststreifen. Solche Vorgänge kann man mit Diffusionsgleichungen aus der Physik berechnen. Zur Abschätzung der unbekannten Faktoren, wie zum Beispiel der Diffusionsrate, muss man dabei allerdings vereinfachende Annahmen machen. Solche unbekannten Faktoren können neuartige, physikalisch inspirierte künstliche neuronale Netze jedoch auch aus Daten lernen. So können Diffusionsprozesse zunehmend akkurat modelliert werden, auch wenn etwa die Diffusionsrate unbekannt ist. Die ersten Versuchsergebnisse sind vielversprechend. Schwer tun sich Wissenschaftlerinnen und Wissenschaftler dagegen bislang beim Versuch, das Verhalten solcher Modelle maschinellen Lernens mathematisch zu fassen.
Aber um welche unbekannten Faktoren handelt es sich in einem Diffusionsprozess? Um das zu verstehen, stellen wir uns einmal einen Unfall vor, bei dem eine große Menge Chemikalien auf einem unversiegelten Boden verschüttet wird. Wie schnell dringen die Schadstoffe nun in den Boden ein, und wie lange bleiben sie dort und stellen somit ein Gesundheitsrisiko dar? Diese Frage rührt an enorm komplexen Vorgängen. Hier kommt uns zum Glück die Physik zu Hilfe mit ihren Gesetzen über das Diffusionsverhalten von Stoffen in einem Medium. Die lassen sich aber nur anwenden, wenn gewisse stoffliche Eigenschaften bekannt sind. Zum Beispiel muss man wissen, wie schnell die Chemikalien bei einer bestimmten Porengeometrie durch den Boden diffundieren. Durch Lernvorgänge erhalten wir mit unserer jüngst entwickelten Methode hierzu nun präzisen Aufschluss. Daraus können wir dann genau abschätzen, wie die Stoffe durch das Medium diffundieren und wie lange sie darin verweilen werden.
Das größere Bild erkennt FINN, ein physik-inspiriertes neuronales Netz
Bei unserem auf der ICML 2022 vorgestellten Ansatz geben bekannte physikalische Gleichungen dem lernenden neuronalen Netz die Richtung vor. FINN, wie der Rufname des „FInite volume Neural Network“ lautet, ist das Kind einer Zusammenarbeit der Forschungsgruppen um Martin Butz (Excellenzcluster “Maschinelles Lernen”, Universität Tübingen) und Wolfgang Nowak (Excellenzcluster SimTech, Universität Stuttgart) unter Federführung der Doktoranden Matthias Karlbauer und Timothy Praditia. FINN ist ein physik-inspiriertes neuronales Netz, das auf die Lösung von Diffusionsgleichungen getrimmt wurde. Als Inspirationsquelle dient ihm dabei das Finite-Volumen-Verfahren aus der computergestützten Physik. Die Allgegenwart von Diffusionsprozessen in der Natur verheißt FINN ein weites Anwendungsfeld.
Soweit wie möglich stützt sich FINN auf bereits bestehende mathematische Gleichungen. Die verbleibende Lücke zwischen Theorie und Praxis schließt FINN dann per maschinellem Lernen. Gelernt werden muss also nur dort, wo die physikalischen Gleichungen die Beobachtungen noch nicht erklären können. Damit diese erlernten Funktionen später interpretiert werden können, muss FINN die existierenden Gleichungen strukturell imitieren. Dazu ist FINN für jede unbekannte Komponente mit einem auf sie spezialisierten Modul ausgestattet (siehe Abbildung 1). Zum Beispiel verfügt FINN über je ein neuronales Netzmodul, um die Diffusionsrate (D), die Geschwindigkeit des Advektionsprozesses (v), oder den Reaktionsprozess (q) zu erlernen.

ABBILDUNG 1: Links: Modularisierungsschema und Informationsfluss bei FINN. Die hier interessierende Größe ist „u“ (z.B. Kaffee, der in einen Cookie diffundiert). In Kreisen sind die trainierbaren Größen dargestellt. Rechts: Advektions-Diffusions-Gleichung mit mehreren Komponenten, die bei FINN in spezialisierten Modulen ihre Entsprechung finden. Einige dieser Komponenten sind typischerweise unbekannt, können aber von FINN erlernt werden.
Das Verzwickte an der Aufgabe ist, dass all diese Prozesse von der diffundierenden Substanz, dem Medium, durch das sie sich bewegt, und den genauen Interaktionen zwischen beiden abhängen. Zu guter Letzt gelang es hier aber dank der Modularisierung, für jede der erlernten Komponenten den genauen Verlauf der physikalischen Funktion zu ermitteln und ihn sogar zu interpretieren (siehe Abbildung 2). Daran sind bisherige Methoden gescheitert.
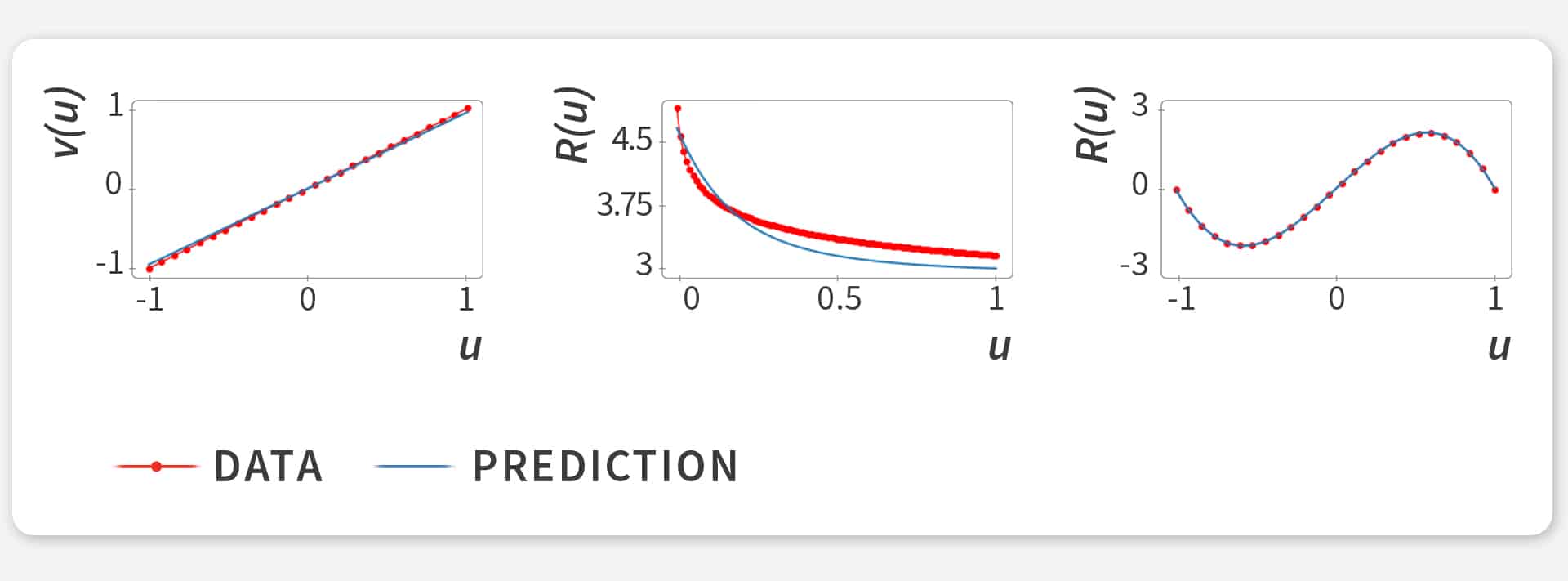
ABBILDUNG 2: In drei Benchmark-Tests musste FINN den Verlauf verschiedener unbekannter Funktionen herausbekommen. Die tatsächlichen Verlaufskurven (rote Linien mit Punkten) stammten jeweils von computergenerierten Daten. Sie waren also bekannt, wurden FINN aber nicht verraten. FINN hat sie jedoch akkurat inferiert (blaue Kurven). Links: Geschwindigkeitsfunktion in der Burgers’-Gleichung. Mitte und rechts: Verzögerungsfaktoren für die Diffusions-Sorptions- und die Allen-Cahn-Gleichungen.
Vorhersage der Diffusion von Bodenschadstoffen
Wir setzten unser Modell ein, um eine Bodenaltlast in der kanadischen Kleinstadt Kitchener zu untersuchen. Dort waren bei einem Zwischenfall auf einem Firmengrundstück in den 1970er Jahren mehrere Kubikmeter der Chemikalie Trichlorethen (TCE) in die Umwelt gelangt. TCE kann DNA-Mutationen, Krebs und Schäden bei ungeborenen Kindern im Mutterleib verursachen. Früher wurden solche Chemikalien oft zur Entfernung von Fetten in der Metallproduktion eingesetzt, da sie Fette sehr gut lösen und schnell verdunsten. Wird TCE jedoch verschüttet, gelangt es in den Boden und diffundiert in die Tiefe bis ins Grundwasser. Aufgehalten wird es erst, wenn es auf undurchlässiges Material trifft – in diesem Fall eine mehrere Meter dicke Lehmschicht. Lehm kann TCE über sehr lange Zeiträume absorbieren. Aber auch in solchen Fällen breitet sich das TCE langsam weiter in der Umgebung aus und kann damit über Jahrzehnte ein ernstes Risiko für die menschliche Gesundheit bergen.
Hier kam FINN ins Spiel. Wir trainierten FINN darauf, die Kontaminationsprozesse zu modellieren. Daraus ließ sich die uns noch unbekannte Diffusionsrate im Boden herleiten, ohne jedwede Vorannahmen treffen zu müssen. (Mit einem konventionellen Modellierverfahren hätten wir uns zum Beispiel auf eine bestimmte Isothermenfunktion für die Sorption festlegen müssen.) Damit konnten wir dann den Diffusionsprozess um fast zwei Monate voraussimulieren und vorhersagen, wie er unter verschiedenen Anfangs- und Randbedingungen verlaufen würde. Solche Informationen sind für die Sanierungsplanung und Risikobewertung hilfreich, da sie treffsicherere Entscheidungen ermöglichen.
Neue Zugänge zum Verständnis von Diffusionsprozessen
Technisch gesehen lässt sich unser Verfahren auf ein breites Spektrum physikalischer Prozesse anwenden. Beispiele sind Wärme- und Schallwellen in der Erdatmosphäre sowie Strömungsphänomene in Rohren oder im Untergrund. Prinzipiell eignet sich FINN dazu, die Diffusion von Stoffen in jedem beliebigen Medium zu charakterisieren. Das steigert die praktische Nutzbarkeit von Strömungsgleichungen ganz erheblich.
Als nächstes Anwendungsfeld haben wir die Wettervorhersage ins Auge gefasst. Dort soll FINN die Bewegung von Teilchen in der Atmosphäre beschreiben und uns so helfen, Prozesse zu verstehen, die die Wissenschaft noch nicht durchdrungen hat.
Originalpublikation:
Übersetzung ins Deutsche: Conrad Heckmann
Titelillustration: Franz-Georg Stämmele

Sehen Maschinen wie Menschen? Immer mehr!

Kommentare