In Platos Höhlengleichnis ist eine Menschengruppe von Kindheit an in einer Höhle eingesperrt. Sie nehmen die Welt nur als Schatten von Objekten auf einer ansonsten leeren Wand wahr. Eines Tages wird einer der Gefangenen freigelassen und kann nun die Welt so erleben wie wir – mit dreidimensionalen Objekten, Farben, Schatten und Licht. Er ist verblüfft von der fundamentalen Verschiedenheit dieser Realität, und man stelle sich vor, er würde zurück in die Höhle gehen und versuchen, diese Welt den verbliebenen Gefangenen zu beschreiben. Das wäre sehr schwierig, denn die Menschen in der Höhle haben nie etwas anderes gesehen als Schatten auf einer Wand.
In ähnlicher Weise geht es beim künstlichen Sehen darum, Maschinen beizubringen, die Welt so zu „sehen“ wie wir. Gewöhnlich geschieht dies, indem der Maschine eine große Anzahl von Bildern gezeigt und sie darauf trainiert wird, aus diesen Bildern Vorhersagen abzuleiten. Aber Bilder sind ja nur eine Projektion der wirklichen Welt, genauso wie die Schatten, die die Gefangenen in Platos Höhle sehen können. Daher ist die Ableitung von 3D-Eigenschaften eine besonders schwierige Aufgabe. Doch für viele nachgelagerte Anwendungen ist die dreidimensionale Erfassung unserer Welt essenziell. Für das autonome Fahren von Fahrzeugen sind dabei Simulationen ein wichtiger Ansatz, um Szenarien zu erzeugen, für die Daten in der wirklichen Welt nur schwer zu bekommen sind. Die Sammlung von echten Daten ist vielleicht aus Sicherheitsgründen unerwünscht, z.B., wenn ein Kind unerwartet auf die Straße rennt. Oder aber bei Szenen, die schwer zu beobachten sind, weil es sich um ein unwahrscheinliches, wenngleich nicht unmögliches, Szenario handelt, etwa wenn ein Zebra vor einem über die Straße rennt.
Das Datenproblem
Wenn Bilder für die Ableitung dreidimensionaler Eigenschaften nicht ideal sind, warum benutzen wir nicht einfach eine große Anzahl von 3D-Objekten und 3D-Umgebungen, um unsere Algorithmen zu trainieren?
Die Antwort ist gleichzeitig einfach und ernüchternd: Weil diese Daten nicht leicht zu bekommen sind. Jedes Smartphone ist zwar mit einer Kamera ausgerüstet, die das Ansammeln von Bildern sehr einfach macht. Aber bei einer 3D-Rekonstruktion müssen die Objekte in der Regel sorgfältig eingescannt werden, indem hunderte von Bildern mit festgelegter Kameraeinstellung aufgenommen werden. Dann müssen diese in 3D so zusammengesetzt werden, dass die Geometrie und Beschaffenheit des Objekts von den verschiedenen Aufnahmen nahtlos miteinander verbunden werden. Das ist ein schwieriger und mühsamer Prozess.
Bilder sind zwar nicht ideal als Trainingsdaten, doch sie können immer noch wichtige visuelle Merkmale übermitteln. Denken wir an das Foto eines Autos in einem Magazin. Wir können uns leicht vorstellen, wie es von hinten aussieht oder auch in einer anderen Farbe. Das ist möglich, weil wir tausende von anderen Autos gesehen und wir eine abstrakte Vorstellung von dreidimensionalen Autos haben, wie den groben Umriss eines Fahrzeugs und Symmetrieregeln. In unserer Arbeit folgen wir dem gleichen Ansatz und trainieren unseren Algorithmus mit tausenden von Bildern unterschiedlicher Autos, von denen er die allgemeinen Eigenschaften eines Autos lernen kann, wie Form oder Erscheinung.
Wie Bilder im Computer entstehen
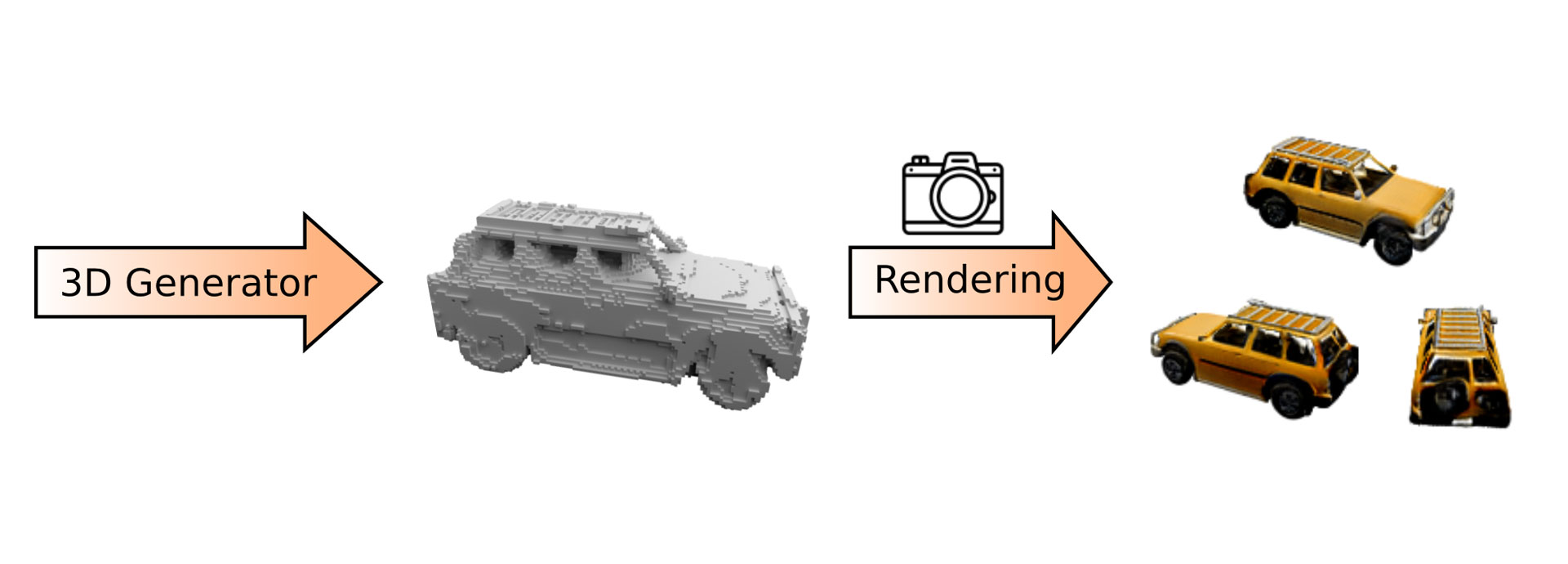
Abb. 1: Unser Algorithmus generiert zunächst ein Objekt. Das Objekt wird dann von einem beliebigen Blickwinkel auf ein zweidimensionales Abbild projiziert.
Während unser Algorithmus zwar lernen soll, 3D-Objekte zu erzeugen, stehen uns nur Bilder als Trainingssignal zur Verfügung. Daher übertragen wir das generierte 3D–Objekt auf ein zweidimensionales Abbild, das wir dann mit einem Bild aus den Trainingsdaten vergleichen. Dieser Projektionsschritt wird ‚rendering‘ genannt, und wird im Algorithmus mit einem virtuellen Kameramodell beschrieben. Abb. 1 zeigt einen schematischen Überblick unseres Algorithmus. Unser Algorithmus erzeugt zunächst ein dreidimensionales Objekt, von dem anschließend ein zweidimensionales Bild gerendert wird. Wir können die virtuelle Kamera dazu in allen möglichen Blickwinkeln positionieren. Auf diese Weise können wir den Algorithmus benutzen, um ein Video zu erstellen (siehe unten).
Rechenaufwand für 3D
Eine weitere Herausforderung bei der Arbeit mit 3D-Daten ist der große Rechenaufwand, der für die Berechnungen notwendig ist. Bilder werden digital auf einem 2D-Raster von Pixeln (Bildelementen) repräsentiert. Nehmen wir ein Bild mit einer Auflösung von 256^2 Pixel. Wenn die Auflösung verdoppelt wird, ergibt das die vierfache Anzahl von Pixeln, nämlich 512^2, d.h., die Anzahl der Pixel wächst quadratisch zur Auflösung. Das 3D-Äquivalent zu Pixel heißt ‚Voxel‘ (Volumenelement). Wenn die Auflösung eines 3D-Voxel-Rasters verdoppelt wird, wächst die Anzahl der Voxel kubisch, d.h. mit einem Faktor von 8. Aus diesem Grund kann die Darstellung von 3D-Objekten in Voxel-Rastern rasch eine extrem hohe Speicherkapazität erfordern.
Die gute Nachricht hierbei ist, dass der Raum bei einer 3D-Darstellung überwiegend leer ist, d.h., bei der Generierung eines Autos auf einer Straße gibt es viel freien Raum, weil es nur wenige andere Autos und andere Objekte gibt und der meiste Raum aus Luft besteht. Außerdem reicht es meist aus, bloß die Oberfläche des Objekts zu modellieren. Daher brauchen wir bei 3D-Rekonstruktionen nicht für jeden Punkt einen Voxel zu speichern. Indem wir unseren Algorithmus so entwickeln, dass er leere Voxel ignoriert, sorgen wir dafür, dass der Rechenaufwand vertretbar bleibt. Abb. 3 zeigt das erstellte Voxel-Raster zusammen mit den generierten Bildern.
Und was kommt als Nächstes?
Mit unserem Ansatz zeigen wir, dass Maschinen in der Tat 3D-Eigenschaften allein durch eine große Anzahl von 2D-Bildern erlernen können. Auf lange Sicht wird es interessant sein, komplexere Szenen und Umgebungen zu erzeugen, mit denen autonome Akteure interagieren können. Eine weitere faszinierende Forschungsrichtung ist die textgesteuerte Bildsynthese. Hier beschreibt der Nutzer mit Worten, was der Algorithmus generieren soll, und das Modell erstellt ein auf dieser Beschreibung basierendes Abbild. Vor kurzem wurde das gleiche Prinzip angewendet, um 3D-Objekte nach Textanweisung zu erstellen – was eine Fülle von kreativen Anwendungen ermöglicht, die Text und Bild kombinieren.
Originalpublikation:
K. Schwarz, A. Sauer, M. Niemeyer, Y. Liao and A. Geiger. VoxGRAF: Fast 3D-Aware Image Synthesis with Sparse Voxel Grids. Advances in Neural Information Processing Systems (NeurIPS), 2022
Paper: https://www.cvlibs.net/publications/Schwarz2022NEURIPS.pdf
Projektseite: https://katjaschwarz.github.io/voxgraf/
Cover illustration: Franz-Georg Stämmele
Übersetzung ins Deutsche: Fortuna Communication

So verbessert maschinelles Lernen die 3D-Bodenkartierung

Sehen Maschinen wie Menschen? Immer mehr!



Kommentare